42.まとめとして放射の基本法則を復習しましょう。

1. ブランクの法則

絶対温度以上の温度を持つ物体はその温度に応じたエネルギーを放射しています。
黒体においてその温度と波長の関係を表したものをブランクの法則といいます。
通常の物質は放射率が1以下ですので黒体のようにきれいな山形の曲線では表されません。
また黒体と同じ温度なら黒体の示す山形の曲線より下に表され絶対に上には行きません。
しかも温度が違っても曲線同士が交わることはありません。
これは重要なことです。
温度が高くなればなるほど放射エネルギーは高くなるので遠赤外線の放射エネルギーも高くなります。
ただ近赤外線と遠赤外線の放射割合で考えると遠赤外線の割合は減っていきます。
実際に遠赤外線を利用する場合は％ではなくエネルギーの強さや量なのでヒーターの温度が高い方が良いと言うことになります。
参考のためHPの遠赤外線の基礎のピーク波長と放射エネルギーの分布を再掲します。

【 ピーク波長と放射エネルギーの分布 】



2. ステファンボルツマンの法則

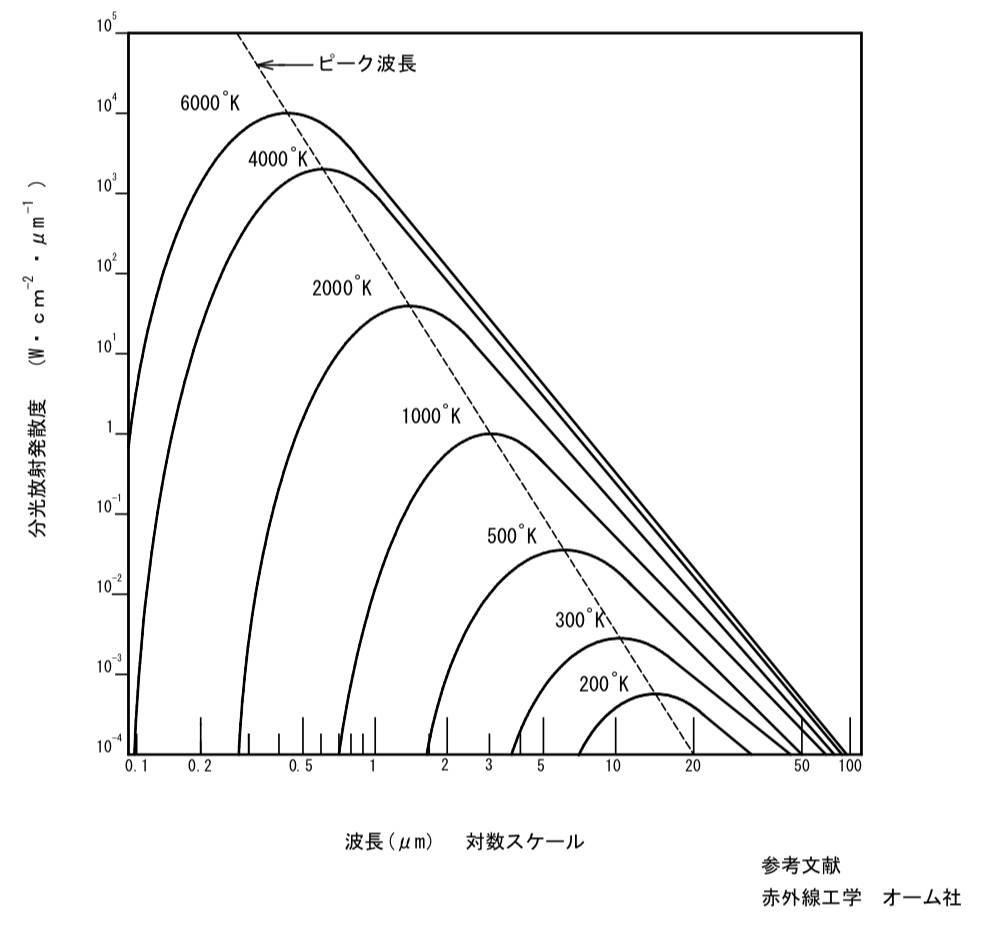
ブランクの法則により放射エネルギーの量は、ヒーターの温度が高くなるにつれ大きくなることは前項で述べました。
放射エネルギーの量は絶対温度の4乗に比例することを表したのをステファンボルツマンの法則といい次式で示されます。

　E＝5.6697＊10⁸＊T⁴　（W／ｍ²）

3. 　ウイーンの変位則

ブランクの法則の図に各温度による放射エネルギーの頂点（ピーク点）を結んだ線があります。
これは放射体の絶対温度が高くなるにつれ、ピーク波長は短波長側に移行することを表しています。

ウィーンの変位則といい、　λ＝2897／T　（μｍ）　で表されます。

グラフのピーク波長から左側（短波長側）と右側（長波長側）の積算エネルギーの比は1：3になります。
ピーク波長を基準に考えると常に長波長側の放射エネルギー量の方が多いと言うことになります。
それも３倍も多いのです。
それではピーク波長を離れて、実際3μ以上の波長を全体エネルギーの5割放射する温度は黒体において約1100℃です。
ウイーンの法則によりこの時のピーク波長は2.1μになります。
すなわち1100℃から放射体の温度が下がるにつれ、遠赤外線が放射エネルギーのなかで割合を増していくことになります。
しかし、実用面では温度が高い放射体の方が遠赤外線放射エネルギーは多くなると言うことを忘れないでください。